Broken Conductors and Negative Sequence Overcurrent Protection

A scenario of nightmares for the Power Systems Engineer is the occurrence of a broken conductor. The vast majority of network protection elements are designed to operate when there is too much phase current, but in the case of a broken conductor it’s the absence of current that is of concern.

Aside from browning-out or shedding downstream loads, broken conductors can cause fire starts and go undetected by conventional overcurrent or earth fault protection relaying techniques. Fortunately, understanding the physics of the broken conductor network scenario is not too difficult, and while three wire and four wire distribution network topologies yield slightly different network responses, a sound understanding of these concepts will help detect and protect against this fault scenario.

Firstly, it’s worthwhile having an understanding of the Fortescue’s Symmetrical Component theory, which we can use to map measured phase currents and voltages to the Positive, Negative and Zero Sequence components. This mapping process allows us to ignore imbalances between phases during faults, making the fault analysis process much easier. Fundamentally, most Alternating Current (AC) protection techniques use this transformation process to detect faults.

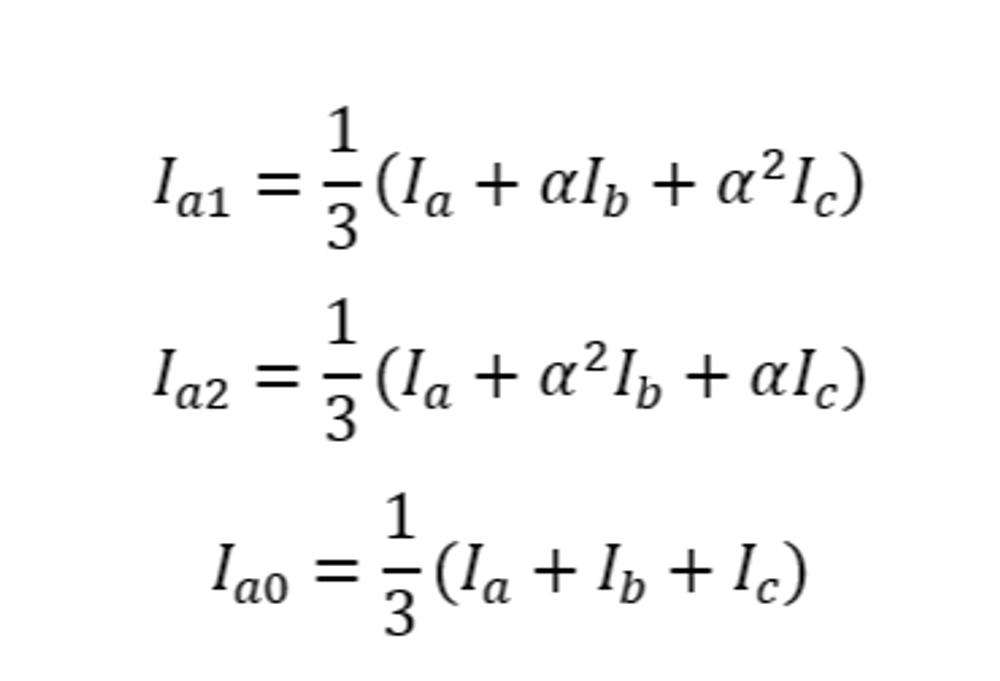
Where:

By entering the values for each phasor measurement, we can derive the magnitude and phase of each of the sequence components. In the ideal theoretical world, a healthy distribution feeder should exhibit no imbalance, and should therefore only have positive sequence current. You can confirm this by substituting in a set of balanced current phasors into the equations and seeing the result adds to zero for every equation except the positive sequence.

In the AC distribution world, symmetrical components aren’t confined to currents alone. Voltages and impedances can also be represented in sequence component format, greatly simplifying fault analysis. A more comprehensive treatise on the subject can be read here: Protection of Electrical Networks , but when we consider the case of broken conductors’ it is important to acknowledge that:

• Voltage Sources are confined to the Positive Sequence elements
• There is equivalent Positive, Negative and Zero Sequence impedance for a distribution network

Three Wire Three Phase Systems

When considering the broken conductor scenario, let’s consider what happens on a three-wire system first.

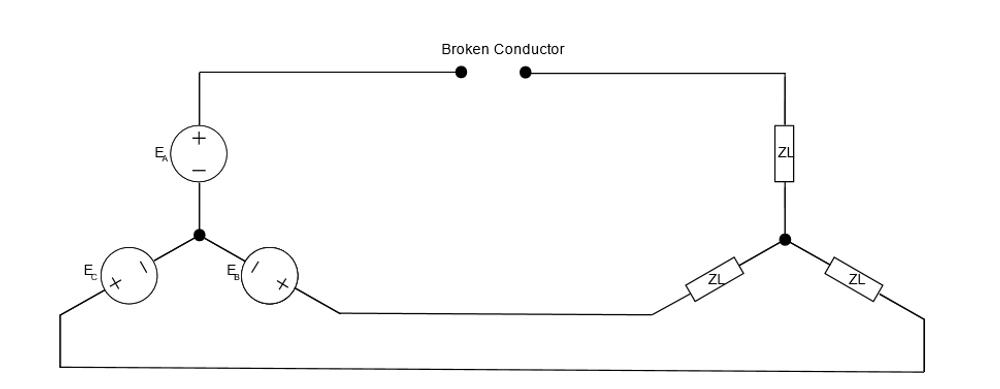
As a first step in analysis, its worth understanding what the broken conductor will mean for each of the phase currents. With a discontinuity in phase A, as shown in figure 1, we effectively remove the current flow through that phase. Despite the 3-phase generators’ efforts to push current through the lines, we can assume that no current flows, leaving us with a clear imbalance. We can rewrite the circuit as follows:

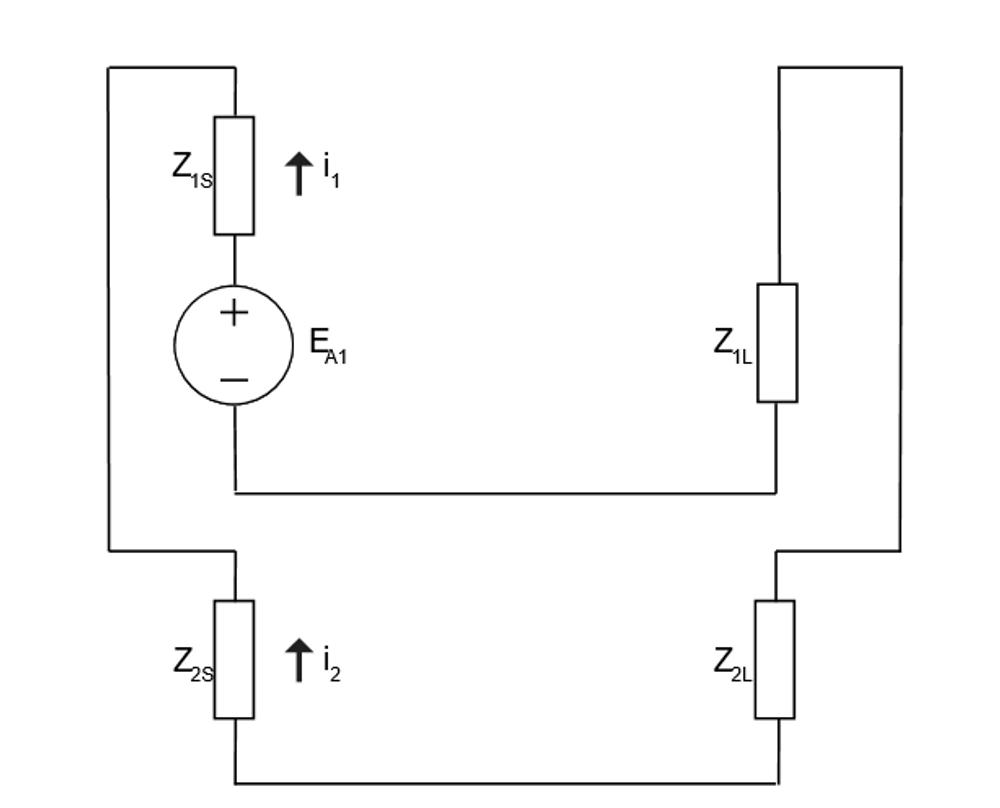
For the seasoned protection engineer, figure 2 greatly resembles the fault analysis of a phase-to-phase fault, which generally makes sense. In a phase to phase fault, the un-faulted phase would seem to have infinite impedance in comparison to a fault between the two other conductors. The only difference is that in a phase to phase fault, we’re only considering the line impedance, while with a broken conductor scenario we are considering the load impedance. As per phase to phase faults, for the broken conductor scenario on a three-phase line our equivalent circuit becomes:

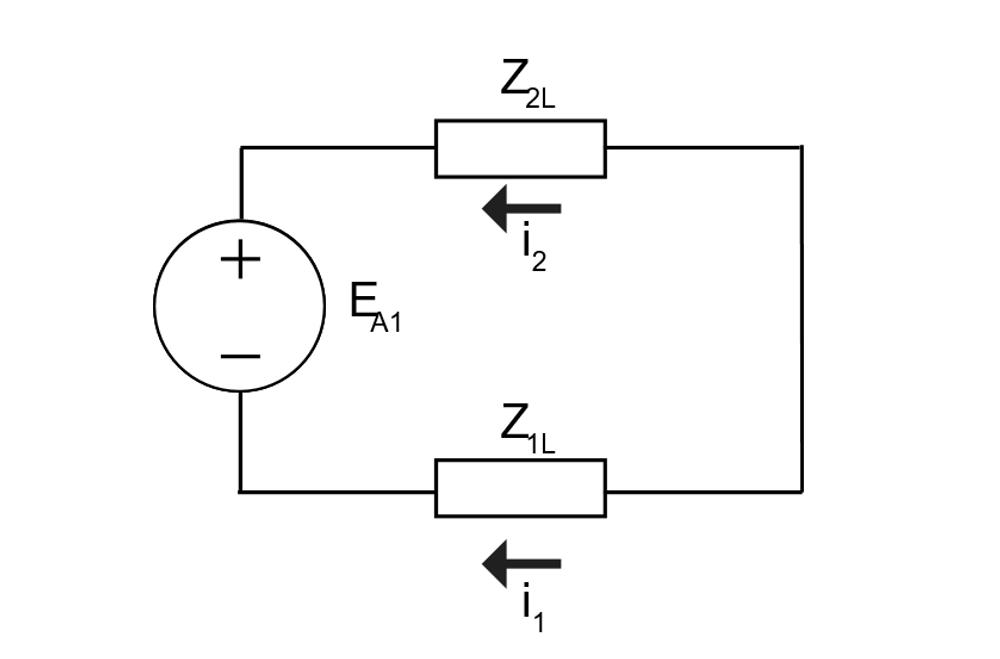
This gives us a few key observations.

1. Under a broken conductor scenario, the positive sequence current is the same as the negative sequence current. When the conductor isn’t broken, its 100% positive sequence and 0% negative sequence.
2. The positive and negative sequence currents are calculated using the same impedance.
3. The load may still be high enough that i1 doesn’t exceed the overcurrent pickup level – dangerous.

Modern digital protection relays often offer both Negative Phase Sequence Protection and Overcurrent protection. For the three-wire case, we can see that the expected negative phase sequence component is dependent on the impedance of the load in the broken conductor scenario. Therefore, the actual resultant negative sequence current depends on the load topology at the time of the fault. For pragmatism, we could consider that in theory a network should exhibit very low negative sequence current in an un-faulted state, so we could plausibly use this as a rationale to set the operating point for NPS quite low. This may work in simple scenarios, but when protection grading between multiple devices becomes an issue, a downstream phase to phase fault in the next zone may appear as an NPS fault in the upstream zone, leading to a race condition between overly sensitive NPS in the upstream device and the conventional overcurrent function in the circuit breaker closest to the fault.

When impedance information is hard to gather, we can rely on the i1 = i2 relationship in a 3 phase system during a broken conductor fault. When a broken conductor occurs, in a perfect theoretical model:

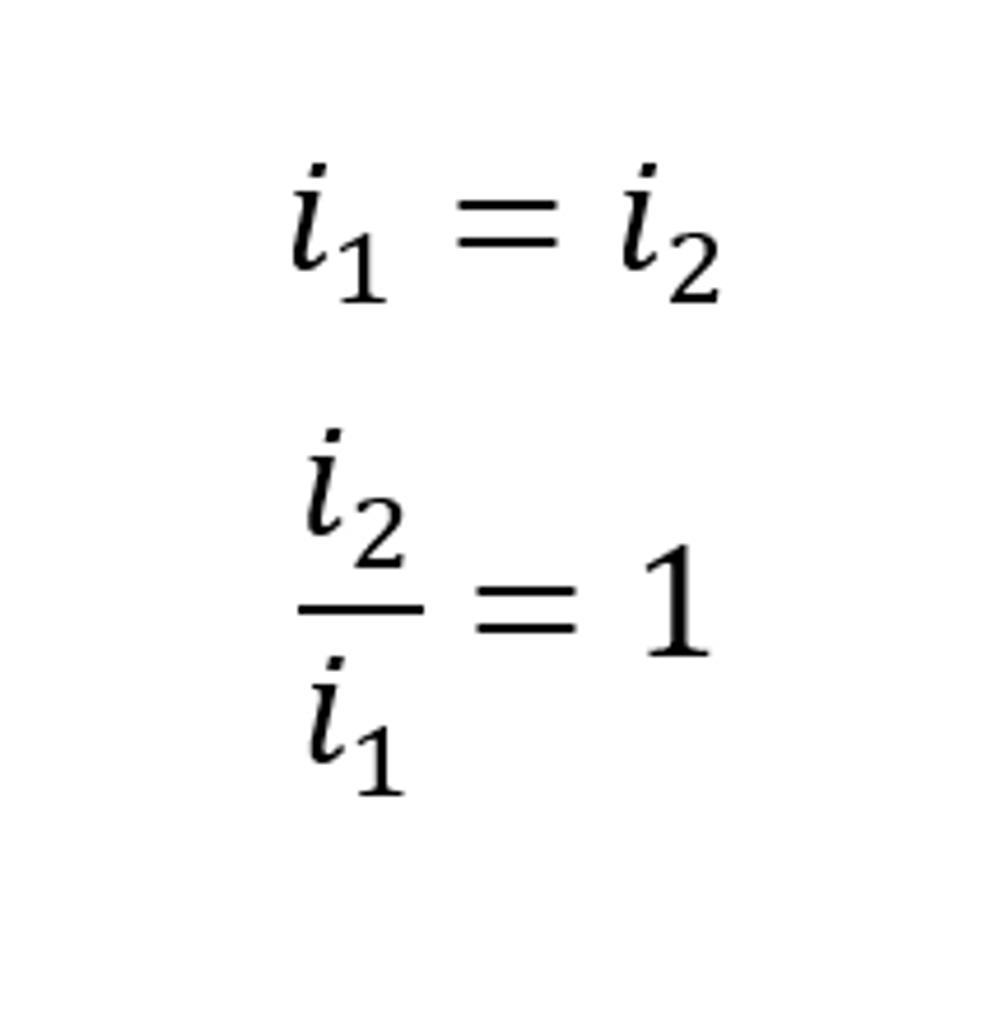
Or expressed in a percentage:

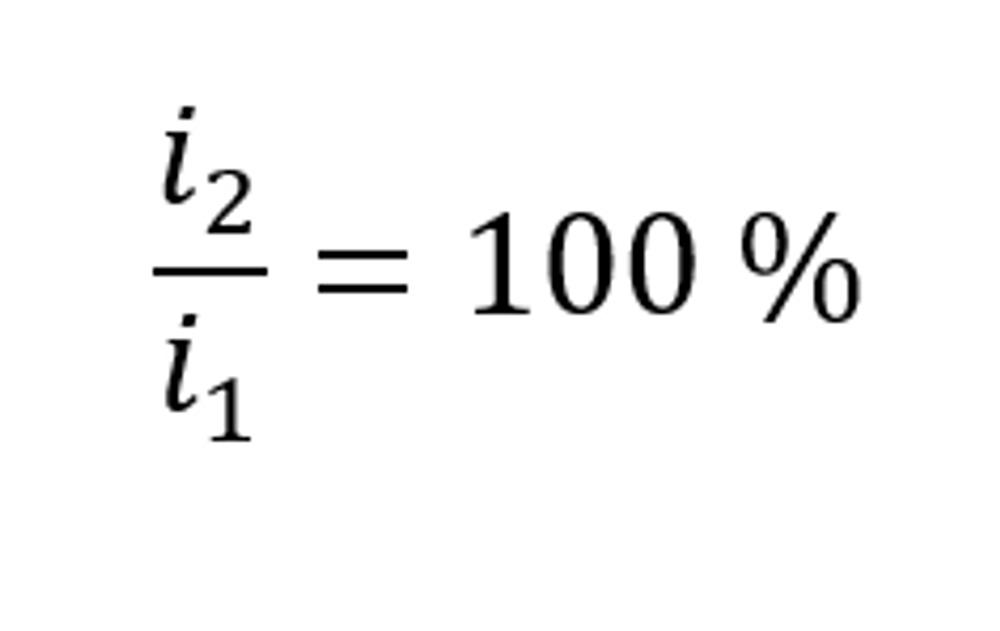
Assigned the ANSI Protection code 46BC (Broken Conductor), this ratio of Negative to Positive sequence removes the dependency of impedance from the calculation. This way, regardless of the load, we have sensitivity to the broken conductor fault condition. To effectively detect the broken conductor scenario in a three-phase network, and it would be very rare for any normal network scenario on a three-phase network to exceed 20% Negative Sequence Current to Positive Sequence. As such, it is a common starting setting for this feature in the field, providing grading with overcurrent elements whilst accounting for the cases of phase discontinuities.

Four Wire Three Phase Systems

Common in North American network topologies and the LV Distribution network in Australia, Four Wire Three phase offers a slightly different result when considering the effects of a phase discontinuity.

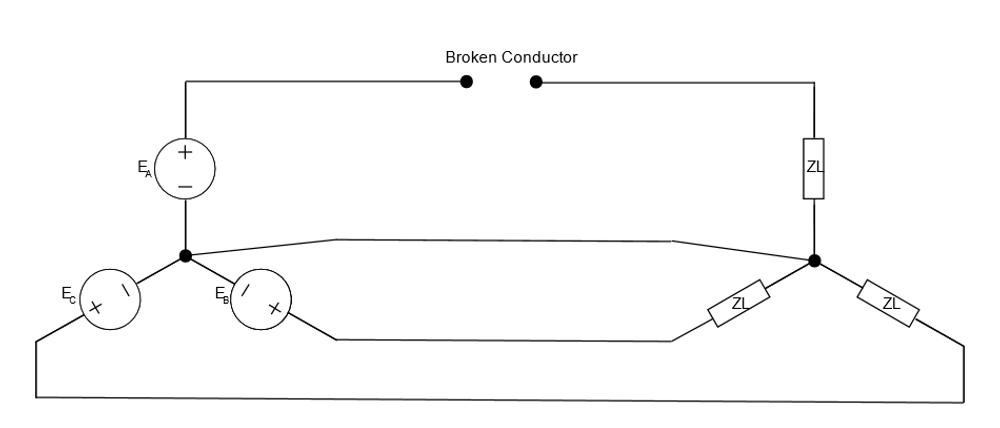
By adding the neutral conductor, we introduce a complication to the calculation because the neutral becomes a current conductor during unbalanced conditions. Oftentimes this is a design consideration, allowing for continuity of service to two thirds of customers in the LV case should a single phase encounter a fault, but by adding the conductor we reduce our ratio of i2 to i1 in the broken conductor scenario. With a neutral conductor in play, we introduce the effect of the zero-sequence impedance:

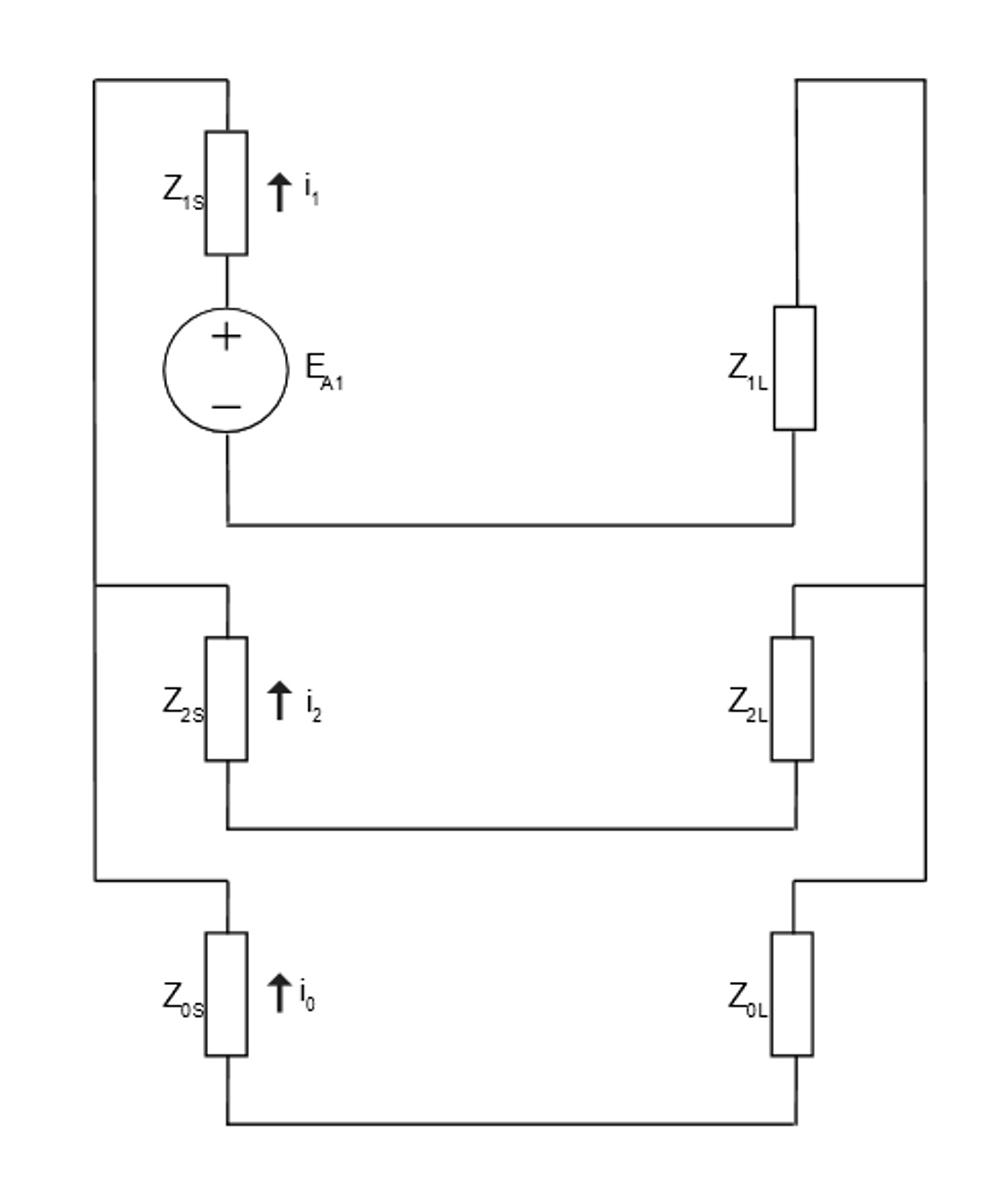
Again, we are faced with an equivalent network that is very similar to the Double Line to Ground fault, except we are considering the load impedances instead of the line impedances. Let’s assume that the source impedances are negligible in comparison to the load, so in simplifying we have:

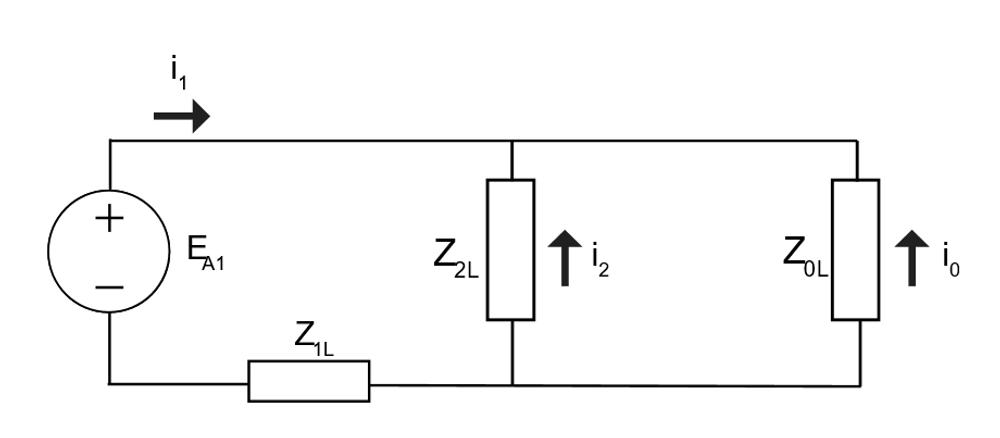
The key difference between the Four wire and Three wire systems in the inclusion of the Zero Sequence in the resultant calculation. Calculating for i1:

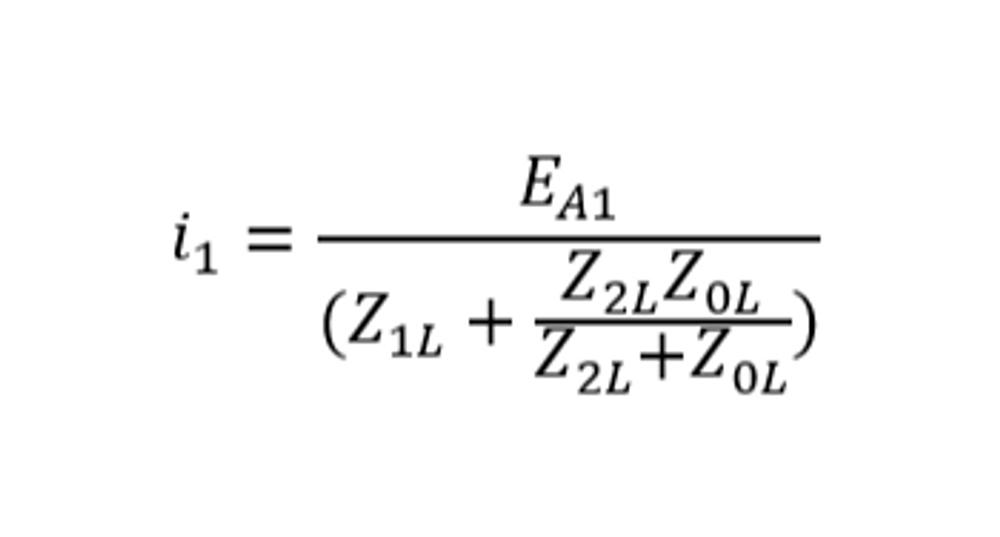
And assuming that i2 is negative and acknowledging the topology as a current divider:

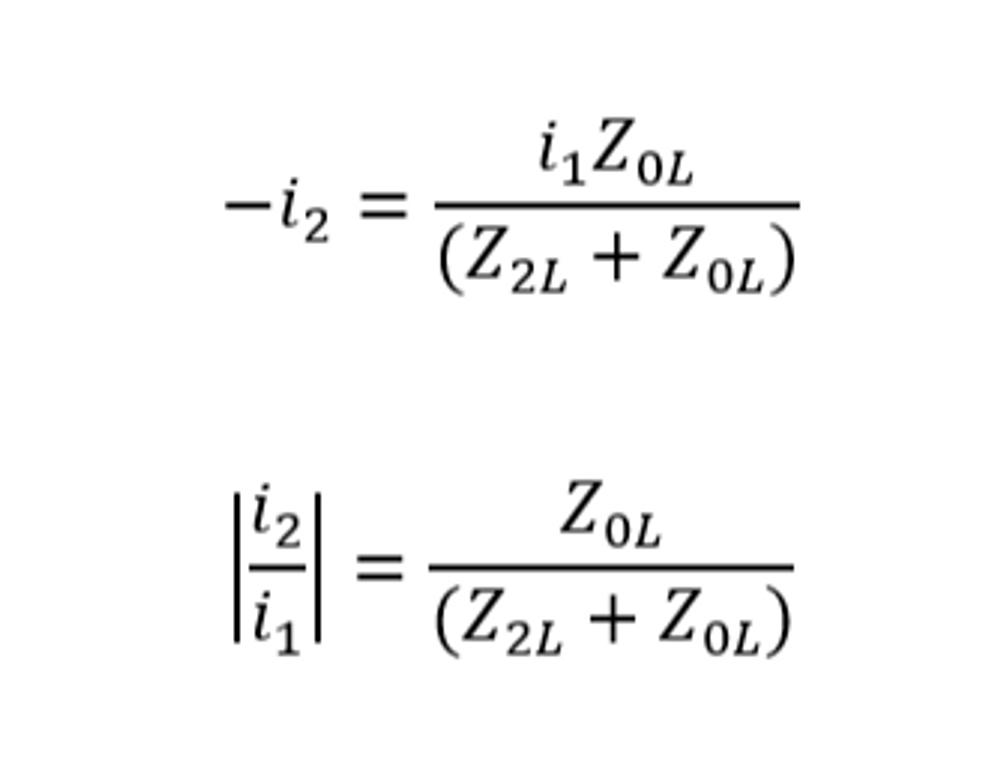
To calculate the minimum broken conductor ratio in a four-wire system, we need to know both the zero and negative sequence load impedance. As a general rule, there is more zero sequence impedance than negative sequence impedance, making the |i2/i1| ratio non-zero, but in the absence of load impedance information it is better to empirically evaluate field data before applying the 46BC feature. Prior service suggests that a 20% |i2/i1| ratio is sufficient on four wire networks for sensitivity but is not immune to spurious tripping in highly unbalanced networks.

“Whilst a complex subject to fully understand, our Broken Conductor detection is simple to setup only requiring the ratio between positive and negative sequence currents to be programmed,” says NOJA Power Group Managing Director, “which we typically recommend to be 20%. It can even be configured to alarm instead of trip to prove the concept in your network.”

Conclusion

Broken conductor detection in the distribution grid is scenario which can be suitably detected through the use of the negative phase sequence current. When using NPS alone, knowledge of the negative sequence impedance of a load is necessary for appropriate calculation. A special case exists for three wire networks, where the positive and negative sequence load impedances cancel out in a phase discontinuity scenario, allowing utilities with 3 wire distribution networks to use |i2/i1| ANSI 46 Broken Conductor protection in the absence of load impedance data.

For 4 wire systems, the calculation becomes marginally more complex, but can be approximated by empirical data giving engineers visibility of the potentially hazardous broken conductor scenario.

NOJA Power’s OSM Recloser system is equipped with a full suite of Negative Phase Sequence and Broken Conductor protection elements, allowing utilities to capitalize on the benefits of their existing asset base and provide sensitivity to this dangerous category of fault for a negligible expenditure.

References

• Elneweihi, A.F., Feltis, M. W., Schweizer, E. O., ©1993, “Negative Sequence Overcurrent Element Application and Coordination in Distribution Protection”, IEEE Transactions on Power Delivery, Vol 8, no 3,
• Prévé, C. ©2006, “Protection of Electrical Networks”, ISTE Ltd, ISBN-13: 978-1-905209-06-04